Закон Ома для полной цепи и для участка цепи: варианты записи формулы, описание и объяснение

Профессиональному электрику, специалисту электронщику никак не обойти в собственной деятельности закон Ома, решая любые задачи, связанные с наладкой, настройкой, ремонтом электронных и электрических схем.

Собственно, понимание этого закона необходимо каждому. Потому что каждому в быту приходится иметь дело с электричеством.

И хотя учебным курсом средней школы закон немецкого физика Ома и предусмотрен, но на практике не всегда своевременно изучается. Поэтому рассмотрим в нашем материале такую актуальную для жизни тему и разберемся с вариантами записи формулы.

Отдельный участок и полная электрическая цепь

Рассматривая электрическую цепь с точки зрения применения к схеме закона Ома, следует отметить два возможных варианта расчета: для отдельно взятого участка и для полноценной схемы.

Расчет тока участка электрической схемы

Участком электрической цепи, как правило, рассматривается часть схемы, исключающая источник ЭДС, как обладающий дополнительным внутренним сопротивлением.

Поэтому расчетная формула, в данном случае, выглядит просто:

I = U/ R,

Где, соответственно:

• I – сила тока;
• U – приложенное напряжение;
• R – сопротивление.

Трактовка формулы простая – ток, протекающий по некоему участок цепи, пропорционален приложенному к нему напряжению, а сопротивлению – обратно пропорционален.

Так называемая графическая «ромашка», посредством которой представлен весь набор вариаций формулировок, основанных на законе Ома. Удобный инструмент для карманного хранения: сектор «P» — формулы мощности; сектор «U» — формулы напряжения; сектор «I» — формулы тока; сектор «R» — формулы сопротивления

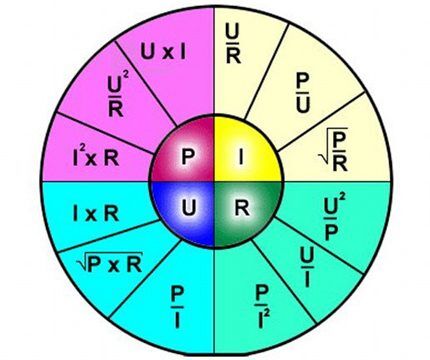
Таким образом, формулой чётко описывается зависимость протекания тока по отдельному участку электрической цепи относительно определенных значений напряжения и сопротивления.

Формулой удобно пользоваться, например, рассчитывая параметры сопротивления, которое требуется впаять в схему, если заданы напряжение с током.

Закон Ома и два следствия, которыми необходимо владеть каждому профессиональному электромеханику, инженеру-электрику, электронщику и всем, кто связан с работой электрических цепей. Слева направо: 1 — определение тока; 2 — определение сопротивления; 3 — определение напряжения, где I — сила тока, U — напряжение, R — сопротивление

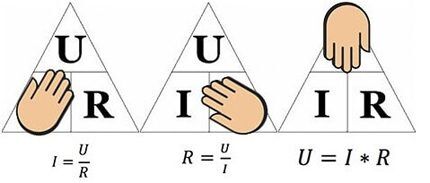
Вышеприведенный рисунок поможет определить, например ток, протекающий через 10-омное сопротивление, к которому приложено напряжение 12 вольт. Подставив значения, найдем – I = 12 / 10 = 1.2 ампера.

Аналогично решаются задачи поиска сопротивления (когда известны ток с напряжением) или напряжения (когда известны напряжение с током).

Тем самым всегда можно подобрать требуемое рабочее напряжение, нужную силу тока и оптимальный резистивный элемент.

Формула, которой предложено пользоваться, не требует учитывать параметры источника напряжения. Однако, схема, содержащая, например, аккумулятор, будет рассчитываться по другой формуле. На схеме: А – включение амперметра; V – включение вольтметра.

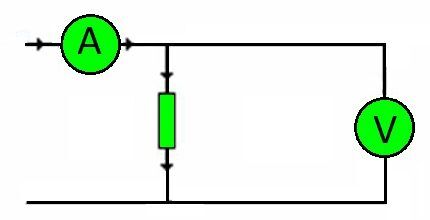
Кстати, соединительные провода любой схемы – это сопротивления. Величина нагрузки, которую им предстоит нести, определяется напряжением.

Соответственно, опять же пользуясь законом Ома, становится допустимым точный подбор необходимого сечения проводника, в зависимости от материала жилы.

У нас на сайте есть подробная инструкция по расчету сечения кабеля по мощности и току.

Вариант расчета для полной цепи

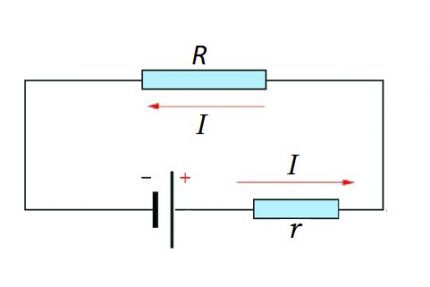
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС.

Поэтому логичным является некоторое изменение выше рассмотренной формулы:

I = U / (R + r)

Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС.

Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.

Для расчетов в условиях полноценной электрической цепи всегда берется к учету резистивное значение источника ЭДС. Это значение суммируется с резистивным сопротивлением непосредственно электрической цепи. На схеме: I — прохождение тока; R — резистивный элемент внешний; r — резистивный фактор ЭДС (источника энергии)

Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины.

Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.

Рассмотрение действия закона к переменной величине

Понятие «сопротивление» к условиям прохождения переменного тока следует рассматривать уже больше как понятие «импеданса».  Здесь имеется в виду сочетание активной резистивной нагрузки (Ra) и нагрузки, образованной реактивным резистором (Rr).

Обусловлены подобные явления параметрами индуктивных элементов и законами коммутации применительно к переменной величине напряжения — синусоидальной величине тока.

Такой видится эквивалентная схема электрической цепи переменного тока под расчет с применением формулировок, исходящих из принципов закона Ома: R — резистивная составляющая; С — емкостная составляющая; L — индуктивная составляющая; ЭДС -источник энергии; I -прохождение тока

Другими словами, имеет место эффект опережения (отставания) токовых значений от значений напряжения, что сопровождается появлением активной (резистивной) и реактивной (индуктивной или емкостной) мощностей.

Расчёт подобных явлений ведётся при помощи формулы:

Z = U / I или Z = R + J * (X_L — X_C)

где: Z – импеданс; R – активная нагрузка; X_L , X_C – индуктивная и емкостная нагрузка; J – коэффициент.

Последовательное и параллельное включение элементов

Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение.

Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.

Цепь последовательно включенных резистивных элементов

Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:

• I = I₁ = I₂ ;
• U = U₁ + U₂ ;
• R = R₁ + R₂

Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения.

Соединение резистивных элементов на участке схемы последовательно один с другим. Для этого варианта действует свой закон расчета. На схеме: I, I1, I2 — прохождение тока; R1, R2 — резистивные элементы; U, U1, U2 — приложенное напряжение

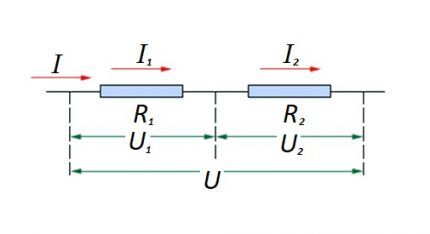
Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.

При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx.

Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.

Цепь параллельно включенных резистивных элементов

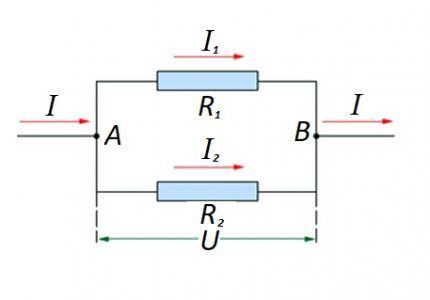
На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:

• I = I₁ + I₂ … ;
• U = U₁ = U₂ … ;
• 1 / R = 1 / R₁ + 1 / R₂ + …

Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение.

Соединение резистивных элементов на участке цепи параллельно один с другим. Для этого варианта применяется свой закон расчета. На схеме: I, I1, I2 — прохождение тока; R1, R2 — резистивные элементы; U — подведённое напряжение; А, В — точки входа/выхода

Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.

Интегральная и дифференциальная формы закона

Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры.

Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.

Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.

Под дифференциальный расчет берется формула: J = ό * E

Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ   

Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.

Выводы и полезное видео по теме

Подробный разбор закона Ома в видеоролике, представленном ниже, поможет окончательно закрепить знания в этом направлении.

Своеобразный видеоурок качественно подкрепляет теоретическое письменное изложение:

Работа электрика или деятельность электронщика неотъемлемо связана с моментами, когда реально приходится наблюдать закон Георга Ома в действии. Это своего рода прописные истины, которые следует знать каждому профессионалу.

Объёмных знаний по данному вопросу не требуется — достаточно выучить три основных вариации формулировки, чтобы успешно применять на практике.

Хотите дополнить изложенный выше материал ценными замечаниями или выразить свое мнение? Пишите, пожалуйста, комментарии в блоке под статьей. Если у вас остались вопросы, не стесняйтесь задавать их нашим экспертам.